Simulation results (at close approach): t=0.930, D_sep=0.007, theta=-0.000, S=13.965, S_AB=9.989, A:(7.448,0.000), B:(7.441,0.000)
Irodov answer (based on computed formula): τ=0.932Irodov Problem 1.13
Let us take a look at Problem 1.13 from the well-known book Problems in General Physics by I.E. Irodov.
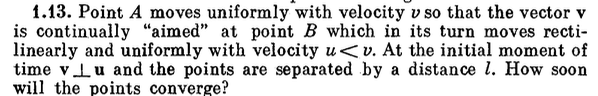
Attempting, getting stuck and then using the hint !
We could think of point A being a missile that tracks and targets a moving object B. B is moving in a straight line with a uniform speed u, and at every instant B is approaching it with the same speed v. The direction of A’s velocity changes at every instant since B is moving. At the start, i.e. \(t=0\), the direction of motion of A is perpedicular to that of B.
It is clear that v > u if the points have to converge, or as per our analogy, if missile A has to hit B.
Let us assume B is heading along the positive x direction with speed u. Then, at \(t=0\), A is moving along the positive y direction with speed v.
We can easily write the equations for the motion of A and B along the x and y direction. Let \(\alpha(t)\) be the angle the velocity vector of B makes with the +x axis at time t. If \(\tau\) is the time it takes for the points to converge, then we have the following equations.
- y direction \[ \int_0^\tau vsin(\alpha(t)) \,dt = l \qquad\qquad (1) \]
- x direction \[ \int_0^\tau vcos(\alpha(t)) \,dt = u\tau \qquad\qquad (2) \]
However, although these equations are correct, determining \(\tau\) by solving these is certainly not straightforward, and possibly not feasible for my level.
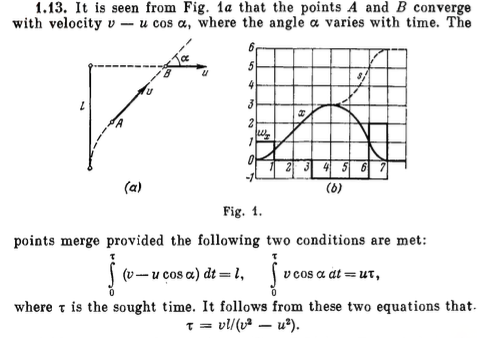
Now, this is one of those rare problems, where the Irodov book itself provides a solution along with the answer ! We show that solution below. Ignore the (b) part of Fig. 1 as that is for a different problem.
Completing the solution
In Irodov’s solution, the second equation is identical to our equation along the x-axis.
However, for the first equation, instead of the y-axis, they consider motion along the line joining A and B at any instant. The interesting thing here is that this line is constantly changing with time as A and B move.
In A’s frame of reference, A is approaching B along a straight line as it is always moving in B’s direction. The speed of approach, as seen by A, varies with time and the distance to B shrinks from l to zero. This speed of approach seen by A is equal to \(v - ucos(\alpha(t))\) at any time t.
The advantage of this formulation is that we can now easily find a simple expression for \(\int_0^\tau cos(\alpha(t)) \,dt\) from the second equation and use it in the first to obtain \(\tau\). That’s indeed a neat mathematical trick !
Let’s write out the steps. Our eqn (1), is now \[ \int_0^\tau v - ucos(\alpha(t)) \,dt = l \qquad\qquad (1) \]
Using eqn (2) \[ \int_0^\tau vcos(\alpha(t)) \,dt = u\tau \] \[ \therefore \int_0^\tau cos(\alpha(t)) \,dt = u\tau/v \qquad\qquad (3)\\ \]
From eqn (1), we have \[ \int_0^\tau v - ucos(\alpha(t)) \,dt = l \] \[ v\int_0^\tau \,dt - u\int_0^\tau cos(\alpha(t)) \,dt = l \\ \]
Using (3), we get \[ v\tau - u^2\tau/v = l \]
\[ \therefore \tau = vl/(v^2 - u^2) \]
Digging deeper
It will be nice to solve the problem through a numeric simulation and visualize the trajectories so that we can see the tracking missile zero in on its moving target ! The folded code block below generates the trajectory data numerically and verifies the time with that obtained from the solution above.
Now we can plot the trajectories using the data generated above.
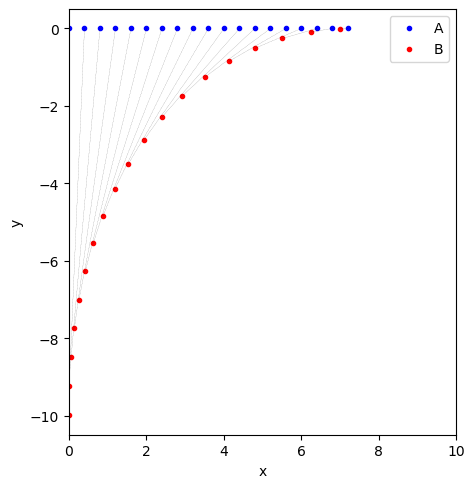
Finally we create an animation to show our missile A track and hit its moving target B !